Autor: Leonardo R. A. X. Menezes

Olhando no Retrovisor – COVID 19 – Parte 1

Bom, como já se passaram alguns anos após a pandemia de COVID-19, creio que é hora de olhar de modo mais crítico o problema dos erros e dos acertos durante o período. Para tanto vamos começar dando uma olhada nos dados que colhemos ao longo da pandemia e depois vamos comparar com as predições.

Primeiro vamos ver o número de casos acumulado durante o período da COVID

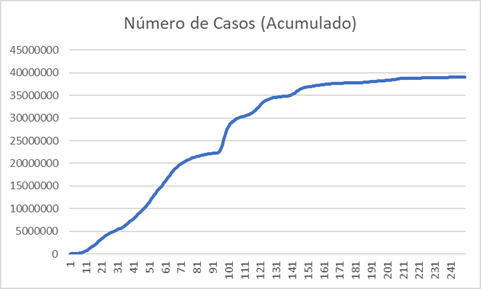
Temos ao final de 2024 o número de cerca de 39 milhões (39.073.544). Bom, isto não são os 2013 milhões de brasileiros, então a primeira pergunta é por quê?

Bom, a resposta é relativamente simples: após um certo tempo nem todas as infecções de COVID eram informadas, e talvez isso seja mais claro no gráfico do número de casos por semana.

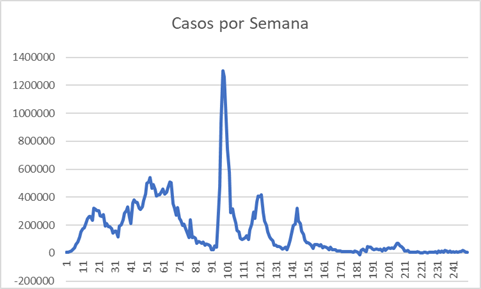
Se olharmos a variação semana a semana fica claro que temos alguns momentos diferentes. Até a semana 94, parece que temos um comportamento mais ou menos esperado de uma doença se difundindo em uma população, mas depois dessa semana temos três picos  bem característicos que indicam algo diferente da infecção inicial. Vamos ver com relação a linha do tempo: a vacinação começou em janeiro de 2021 (mais ou menos na semana 44) e em setembro de 2021 cerca de 80-90% da população tinha sido ao menos parcialmente vacinada (mais ou menos na semana 77). Assim até a última semana de 2021 (semana 94) temos mais ou menos o comportamento esperado.  Mas então temos três picos : semana 98 (1.30 milhões), semana 120 (409 mil) e semana 144 (321 mil). As razões para esses picos? Francamente não sei… Mas tenho suspeitas…

Além do número de casos temos ainda o número de óbitos. Algo que durante muito tempo foi elemento de grande contestação.

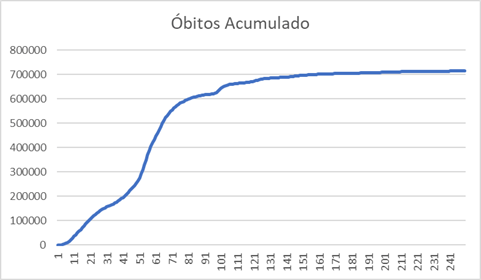
Mas para vermos melhor vamos colocar as curvas de casos e óbitos acumulados na mesma escala e em conjunto

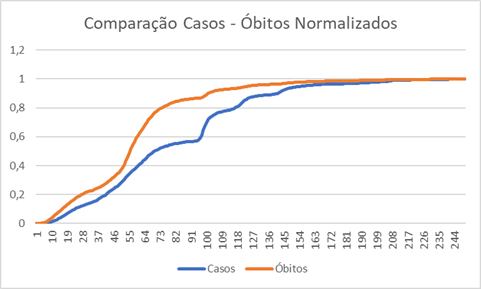
Aqui as coisas começa a ficar estranhas: o número de óbitos pré-data o número de casos. Normalmente o que esperamos é que o número de casos aumente e isso seja seguido por um aumento no número de óbitos. Isso só é o caso quando temos vacinação antes, assim o número de óbitos acumulado se estabiliza em um máximo enquanto o número de casos acumulados ainda vai aumentar mais. Mas isso é o que se espera após uma vacinação. Vamos dar uma olhada no número de óbitos a cada semana

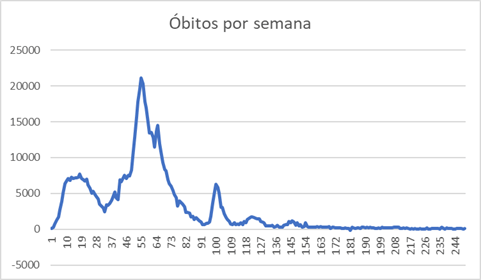
Esta curva é bem diferente da curva dos números de casos a cada semana. Para começar, depois da semana 91, os picos são substancialmente menores e ocorrem em pontos diferentes. Os picos de casos infeção após a semana 91 ocorreram na semana 98 (1.30 milhões), semana 120 (409 mil) e semana 144 (321 mil). Já os picos de óbito ocorreram nas semanas 100 (6.3 mil), semana 122 (1.7 mil) e 146 (1.2 mil)

Vamos ver os dois gráficos em conjunto, e com normalizados de modo apropriado (cada um dividido pelo seu número final).

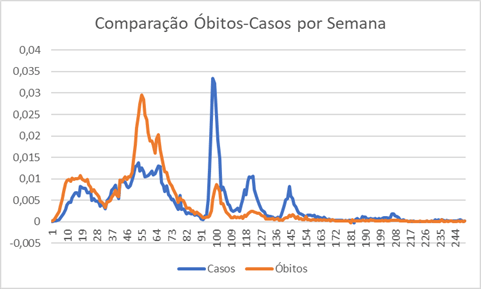
Aqui temos algumas informações interessantes, sendo a primeira é que a taxa de mortalidade varia ao longo do período, sendo maior até a semana 91 e bem menor depois disso. Há também algo estranho no início da pandemia: até a semana 37, a mortalidade parece preceder o aumento no número de casos. Isso em parte pode ser explicado se houver sub notificação no início da pandemia (ou mais especificamente se há alguma dificuldade em associar a causa da morte a COVID).

o primeiro grande salto começa na transição da última semana de 2021 para primeira semana de 2022 (de 40 mil para 208 mil). Aqui é que eu tenho uma suspeita: não temos uma única infecção de COVID, sendo que algumas se misturam. Temos aproximadamente:

  1. Uma infecção da semana 1 até a 30
  2. Uma infecção da semana 30 até 91
  3. Uma infecção da semana 91 até 109
  4. Uma infecção da semana 109 até 117
  5. Uma infecção da semana 136 até 154

Podemos usar o modelo SIR mais simples para ver como seria o comportamento em uma pandemia. É isso é que vou fazer em um próximo post.

Um mar morto de links ou um mar de links mortos

Depois de muito tempo, estou de volta.

Tanta coisa aconteceu, fica até difícil resumir tudo. 

Então vou fazer diferente, vou revisitar meus artigos antigos que considero mais interessantes e fazer atualizações deles. Aqui e na nova versão do blog.

O que descobri é que a internet não é um oceano de memórias, mas um mar de links mortos.  Olhando meus artigos postados desde o início do blog, o que vejo é que enorme maiorias dos links estão mortos.

Mortos no sentido de não estarem mais ligados a nada. A minha ilusão que a internet ia ser um repositório de ideias, que poderíamos acessar as partes relevantes simplesmente clicando em alguns links, foi tudo por água abaixo.

Em retrospecto, penso que eu deveria ter esperado isso: Servidores são desativados, programas são atualizados, o espaço de armazenamento é finito e assim vai. Então temos posts aqui cujas referências se desmancharam, cujos links com mais detalhes não existem mais, cujos vídeos foram retirados, cujas músicas sumiram, que os plug-ins não funcionam mais…

E nem vou entrar na questão dos links que sumiram por decisões judiciais (embora talvez devesse).

Em resumo, a internet não é aquilo que imaginei que seria: um repositório, uma fonte de conhecimento, um modo de guardarmos as memórias do que fizemos, tivemos ou vivemos.

Isso é um pouco triste, um pouco desalentador…

Para os políticos…

Depois de agonizar sobre os números da pandemia de COVID 19, resolvi transformar os números em algo que os políticos podem entender: número de eleitores.

A ideia é que os doentes e mortos não existem em um universo separado. Na realidade, cada um tem família e amigos. Ou seja, gente que se importa pelo fato de que esse pessoal sofreu ou mesmo faleceu com a doença. E possivelmente vão se lembrar disso nas próximas eleições.

Para simplificar a análise trato do número de falecidos, e da probabilidade, que nada mais é que o número de mortos por milhão dividido pelo número de milhões que o país tem.

Então, no momento, há 1225 mortos por milhão no Brasil. Isto corresponde a um percentual de mortos de .5805687204e-3 ou 0.0006% da população total aproximadamente.

Naturalmente, os mortos não votam. Mas seus parentes e amigos sim. Então considerando os grupos de Whatsapp familiares,vamos ver a chance que em um grupo de 50 pessoas, pelo menos uma tenha morrido de COVID.

1-(1-p)^50 = 0.029 que é aproximadamente 0.03 ou 3%

Isto permite o cálculo do número esperado de pessoas no Brasil que está nessa situação. Este número é de seis milhões de pessoas. E um percentual significativo destes culpará os governantes pelas mortes.

Esse percentual não vai esquecer e não vai deixar que ninguém se esqueça. Tanto faz se a eleição é em 2022, 2024 ou 2026. Não irão esquecer que parte destes mortos poderiam estar vivos agora, mesmo que isso não faça sentido. Afinal, faz mais sentido culpar um governante pelos erros cometidos no combate a pandemia. E quem vai dizer que a culpa está na pessoa errada? Não é um discussão racional (mesmo porque os governantes cometeram muito erros mesmo, e o presidente tem destaque nisso).

Esses, além de eleitores, podem afetar a eleição. Não é improvável que este pessoal ajude a transformar a imagem de um candidato em inimigo do povo. E não vai ter adiantar televisão, rádio ou internet para mudar isso – aqui o caso é, possivelmente, sangue nos olhos ou mágoa no coração.

Esta é, aproximadamente, a situação atual.

Mas o que acontece se esse percentual dobrar? Aí o número sobe para 12 milhões (o que significaria cerca de 500 mil mortos). Isto corresponderia a uma taxa de 2250 por milhão. Na amazônia, esta taxa se encontra em 2657 por milhão. E aí…

Então, srs. governantes, é bom ficarem espertos… Pois esse pessoal não esquece, e não deixa ninguém esquecer…

Quantas pessoas que você conhecem podem estar doentes?

Prezados, depois de um bom hiato, e de descobrir que meu antigo blog ainda pode ser utilizado para novas mensagens, eu estou de volta.

Nesses tempos de COVID-19 (COronaVIrus Disease 2019), há muitos conceitos de biologia, química, matemática, estatística e mesmo engenharia flutuando no ar. E um dos tópicos que desejo tratar aqui é sobre a questão de uma unidade relativa ao assunto: infectados por milhão de habitantes (NIpm).

Esse número é, na realidade, uma medida equivalente a probabilidade (população dividido por população). E pode estar relacionado a chance que você conheça alguém com a doença.

Como a probabilidade de alguém estar infectado pode ser descrita, de modo simplificado, como o número de infectados (NI) dividido pela população geral (NT), ou seja: p=NI/NT.

Já o número de infectados por milhão é igual a p*100000. Ou seja NIpm=p*1000000. Assim, p=NIpm/100000. Portanto, para obter a probabilidade de alguém estar infectado é simplesmente o número de infectados por milhão, dividido por 1 milhão .

Então como utilizar isso? Vamos dizer que haja aleatoriedade em que você conheça alguém que tem ou não a doença. O conjunto é (p+q)=1, aonde p é a probabilidade de ter a doença e q é 1-p. Portanto, ao encontrar aleatoriamente n pessoas, temos o binômio de Newton (p+q)^N. No caso de duas pessoas (N=2), podemos expandir com facilidade:

p^2+2*p*q+q^2

Já a chance que nenhuma dessas pessoas tenha a doença é q^2. Ou, seja a chance que uma ou mais delas tenha a doença é 1-q^2=1-(1-p)^2.

O mesmo raciocínio pode ser utilizado se temos N pessoas, neste caso a probabilidade é 1-(1-p)^N.

Para valores pequenos de p (ou seja, quando o número de infectados por milhão é pelo menos 100 vezes menor que 1 milhão), esta expressão pode ser aproximada por:

1-1+N*p=N*p

Lembrando que NIpm=p*1000000, portanto a chance pode ser aproximada por N*NIpm/1000000

Bom, aí quando é que esta chance é de 50%?  É quando N*NIpm/1000000=1/2. Rearranjando:

N=500000/NIpm

Colocando números, se NIpm=50, com 10000 amigos há uma chance de 50%. Com 500, o número de amigos passa a ser 1000. Ou seja, considerando um processo aleatório, se você tiver 1000 conhecidos se o número de infectados por milhão exceder 500, então há uma chance de 50% que algum dos seus conhecidos tenha a doença.

Bom e como estão os números hoje (28 de maio de 2020)? Existem cerca de 220 mil casos ativos. Se arredondarmos a população brasileira para 220 milhões isto significa 1 caso em mil. Ou, em termos de infectado por milhão, temos NIpm=1000.

Utilizando as equações temos: N*1000/1000000=1/2, ou N=500. Ou seja se você tem 500 amigos, há uma chance de 50% de pelo menos um deles estar infectado.

 

Mais em estatística

Um ponto interessante sobre a estatística é que a medida que vamos obtendo mais pontos, acabamos por saber mais sobre o que não se encaixa nos dados que estamos calculando.

Ficou confuso?

Vamos a um exemplo para clarificar.

Supondo que obtermos um conjunto de pontos aleatoriamente, como por exemplo: 10, 22, 12, 64, 33 16 e 41.

A estatística dá ferramentas para saber que o valor médio deste conjunto está entre o menor número (10) e o maior número (64), com um probabilidade de 1- (7+1)/(2)^(7-1) ou 0.875. Ou seja, há uma chance de cerca de 7/8 que a média esteja entre o maior número deste conjunto e o menor número deste conjunto.

E isto fica mais impressionante a medida que se aumentam os números. Por exemplo, no caso de 12 amostras aleatórias, a probabilidade é de mais de 99% que a média esteja entre o maior valor e o menor valor.

A chave para derivação deste probabilidade é aleatoriedade na escolha destes pontos. E nisto não há necessidade de levar em conta a distribuição de probabilidade, ou seja, isto vale independente da distribuição.

Maravilhas da Estatística – II

Este post foi originalmente publicado em 12/03/2013

Como o leitor viu no post anterior, a estatística permite inferir informações que poderíamos considerar inacessíveis.

Vamos ver outro exemplo de contagem que permite estimar quantas espécies existem em um determinado nicho ecológico. O processo é conhecido como marcar e recapturar.

Funciona assim: primeiro o pesquisador vai ao nicho ecológico, captura M espécimes e depois os solta na população geral. Em uma segunda visita, ele captura C espécimes e verifica quantos destes foram originalmente marcados. Digamos que este número seja K.

Como o percentual de animais marcados em comparação com a população N é M/N, e se a segunda captura for completamente aleatória então o percentual de animais marcados na amostra C deve permanecer mais ou menos o mesmo. Isto quer dizer que:

M/N deve ser aproximadamente igual a K/C. Assumindo a igualdade, temos M/N = K/C então N = M*C/K

Um exemplo numérico pode esclarecer muito: Vamos dizer que na primeira visita marcamos M=10 espécimes, na segunda visita capturamos C=100 espécimes, dos quais K=2 eram marcados. Isto quer dizer que a população deve ser aproximadamente:

N = 10*100/2 = 500

Podem testar no MATLAB que funciona bonitinho. Naturalmente isto é uma aproximação (afinal supõe que nenhum dos animais marcados morreu ou sumiu no período), mas pode ser usado para estimar populações dos mais diversos tipos (pessoas com doenças na população geral, estimar mercados, etc…). Caso se mantenha um histórico de marcar e recapturar é possível montar uma história com taxa de desaparecimento, taxa de natalidade, entre outras informações.

Maravilhas da Estatística – I

Este post foi originalmente publicado em 10/03/2013

A Estatística permite tomar decisões e estimar dados em situações que parecem impossíveis de se conhecer algo sobre o problema.

Caso em questão? Considere um saco com bolas numeradas de 1 até N. Agora você retira K bolas do saco. Sabendo o número de cada bola será que temos condições de estimar o número total de bolas originamente no saco (N)?

Bem, parece impossível, não? Mas há algumas informações que já temos disponíveis. A primeira é que a densidade de probabilidade é uniforme, ou seja a probabilidade de tirar qualquer bola é 1/N.

O valor médio desta distribuição é:

E{x} = 1/N*(1+2+3+..N) = 1/N*(N*(N+1)/2) = (N+1)/2

 

Então, na realidade, o que queremos é estimar a média, pois:

N=2*E{x}-1

 

Então podemos utilizar um estimador simples de média:

M=1/K*(B1+B2+…+BK)

 

Portanto N=2*M-1

 

Vamos ao teste? Vou considerar um saco com 100 bolas (numeradas de 1 a 100) e extrair 10 bolas aleatoriamente (óbvio que usei o MATLAB). Os números extraídos são:

55 24 62 63 53 59 52 93 20 66

A média deles é: 54.7

Portanto a nossa estimativa de N é 108.4

E se fossem apenas 5 bolas? O valor estimado de N seria de 101.8

A estimativa pode ser melhorada se incluirmos o desvio padrão. Mas para os fins de cálculo simples, este valor está de bom tamanho.

Mas para que serve isso, o caro leitor pode se perguntar? Bom, este tipo de problema é conhecido como Problema do Tanque Alemão. E como o nome indica, a estatística foi utilizada para descobrir quantos tanques alemães estavam sendo fabricados.

A idéia pode ser aplicada para um número de casos (por exemplo: quantas torradeiras de determinada marca são fabricadas, ou quantos IPhones, ou afins).

Realmente extraordinário.

Enigmas Matemático

Mais um dos antigos posts do blog

Faz tempo que estou querendo colocar este post aqui (com sua solução):

Três amigos foram jantar em um restaurante e pediram uma pizza de R$22,00 mais três refrigerantes de R$1,00 cada. Na hora de pagar, cada um entregou para o garçom 10 reais para pagar a conta de R$25,00. O garçom devolveu 5 reais de troco em notas de R$1,00. 

Ao pegar o troco do garçom, os amigos decidiram dar R$2,00 de gorjeta para a divisão entre eles ficar inteira de 1 real para cada. 

Se cada um deu R$10,00 (R$30,00 ao total), recebeu troco de R$1,00, significa que pagaram juntos R$27,00 mais os R$2,00 da gorjeta, resultando R$29,00. Onde está esse 1 real que falta?

O que está errado? Vamos a matemática:

  • X – o que cada um pagou
  • C – Conta
  • T – Troco total

Temos 3*X -C = T, ou 3*10- 25 = 5 – ou seja: Cada um pagou R$ 10,00 e com a conta de R$ 25,00 tivemos um troco total de R$ 5,00
Ok até agora, não?

Mas vamos complicando

  • GG – gorgeta do garçom
  • TI – Troco individual

GG+3*TI = T ou 2+3*1 = 5 – ou seja: dos R$ 5,00, o garçom pegou R$ 2,00 e devolveu R$ 3,00 (R$ 1,00 para cada um).

Juntando as duas expressões temos:

3*X-C = GG+3*TI

Reescrevendo: 3*(X-TI) = C+GG, ou 3*(10-1) = 25+ 2 – ou seja cada um pagou, efetivamente R$ 9,00, e dos R$ 27,00 totais, R$ 25,00 foi para o dono do bar e R$ 2,00 para o garçom.

  • Bar: C+GG  – Conta + Garçom = R$ 25,00 + R$ 2,00 = R$ 27,00
  • Clientes: 3*(X-TI) – o que cada um efetivamente pagou = R$ 9,00+ R$ 9,00 + R$ 9,00 = R$ 27,00

Percebeu aonde esta o erro do enunciado? “Se cada um deu R$10,00 (R$30,00 ao total), recebeu troco de R$1,00, significa que pagaram juntos R$27,00 mais os R$2,00 da gorjeta”

O erro é o seguinte: Os R$ 2,00 de gorjeta estão incluídos nos R$ 9,00 e não fora dele. Cada um pagou R$ 9,00, totalizando R$ 27,00. Destes R$ 27,00, R$ 25,00 foram para o dono do bar e R$ 2,00 foram para o garçom.

Em termos matemáticos a expressão:
Se cada um deu R$10,00 (R$30,00 ao total), recebeu troco de R$1,00, significa que pagaram juntos R$27,00 mais os R$2,00 da gorjeta quer dizer 3*(X-TI)+GG e não 3*(X-TI)-GG (que é a equação original e correta!).

O que isto quer dizer? Que somamos R$ 2,00 ao invés de subtrairmos R$ 2,00. Não tem absolutamente nada a ver com dízima periódica, descontinuidade da função e outras “explicações” que rolam por aí.

Enigmas Matemáticos 1

Mais um post do antigo blog!

OS TRINTA E CINCO CAMELOS – Malba Tahan
Poucas horas havia que viajávamos sem interrupção, quando nos ocorreu uma aventura digna de registro, na qual meu companheiro Beremiz, com grande talento, pôs em prática as suas habilidades de exímio algebrista.
Encontramos, perto de um antigo caravançará meio abandonado, três homens que discutiam acaloradamente ao pé de um lote de camelos. Por entre pragas e impropérios, gritavam possessos, furiosos:
— Não pode ser!
— Isto é um roubo!
— Não aceito!
O inteligente Beremiz procurou informar-se do que se tratava.
— Somos irmãos — esclareceu o mais velho — e recebemos como herança esses 35 camelos. Segundo a vontade expressa de meu pai, devo eu receber a metade, o meu irmão Hamed Namir uma terça parte, e ao Harim, o mais moço, deve tocar apenas a nona parte. Não sabemos, porém, como dividir dessa forma 35 camelos. A cada partilha proposta, segue-se a recusa dos outros dois, pois a metade de 35 é 17 e meio! Como fazer a partilha, se a terça parte e a nona parte de 35 também não são exatas?
— É muito simples — atalhou o “homem que calculava”. — Encarregar-me-ei de fazer com justiça essa divisão, se permitirem que eu junte aos 35 camelos da herança este belo animal, que em boa hora aqui nos trouxe.
Neste ponto, procurei intervir na questão:
— Não posso consentir em semelhante loucura! Como poderíamos concluir a viagem, se ficássemos sem o nosso camelo?
— Não te preocupes com o resultado, ó “bagdali”! — replicou-me, em voz baixa, Beremiz. — Sei muito bem o que estou fazendo. Cede-me o teu camelo e verás, no fim, a que conclusão quero chegar.
Tal foi o tom de segurança com que ele falou, que não tive dúvida em entregar-lhe o meu belo jamal, que imediatamente foi reunido aos 35 ali presentes, para serem repartidos pelos três herdeiros.
— Vou, meus amigos — disse ele, dirigindo-se aos três irmãos — fazer a divisão justa e exata dos camelos, que são agora, como vêem, em número de 36.
E voltando-se para o mais velho dos irmãos, assim falou:
— Deves receber, meu amigo, a metade de 35, isto é, 17 e meio. Receberás a metade de 36, ou seja, 18. Nada tens a reclamar, pois é claro que saíste lucrando com esta divisão.
Dirigindo-se ao segundo herdeiro, continuou:
— E tu, Hamed Namir, devias receber um terço de 35, isto é, 11 e pouco. Vais receber um terço de 36, isto é, 12. Não poderás protestar, pois tu também saíste com visível lucro na transação.
E disse, por fim, ao mais moço:
— E tu, jovem Harim Namir, segundo a vontade de teu pai, devias receber uma nona parte de 35, isto é, 3 e pouco. Vais receber um terço de 36, isto é, 4. O teu lucro foi igualmente notável. Só tens a agradecer-me pelo resultado.
Numa voz pausada e clara, concluiu:
— Pela vantajosa divisão feita entre os irmãos Namir — partilha em que todos os três saíram lucrando — couberam 18 camelos ao primeiro, 12 ao segundo e 4 ao terceiro, o que dá um total de 34 camelos. Dos 36 camelos sobraram, portanto, dois. Um pertence, como sabem, ao “bagdali” meu amigo e companheiro; outro, por direito, a mim, por ter resolvido a contento de todos o complicado problema da herança.
— Sois inteligente, ó estrangeiro! — confessou, com admiração e respeito, o mais velho dos três irmãos. — Aceitamos a vossa partilha, na certeza de que foi feita com justiça e eqüidade.
E o astucioso Beremiz — o “homem que calculava” — tomou logo posse de um dos mais belos camelos do grupo, e disse-me, entregando-me pela rédea o animal que me pertencia:
— Poderás agora, meu amigo, continuar a viagem no teu camelo manso e seguro. Tenho outro, especialmente para mim.
E continuamos a nossa jornada para Bagdá.

Muito bem, o que aconteceu aqui? Que mágica foi essa? Ah, não há mágica nenhuma: a partilha é que não “cobria” todos os animais.

Vamos dizer que tivéssemos X camelos. O irmão mais velho receberia X/2, o do meio X/3 e o mais novo X/9.

Para simplificar vamos dizer que X fosse igual a 18. Assim o irmão mais velho receberia 9, o do meio 6 e o mais novo 2. Note que 9+6+2 é 17 e não 18. Isto significa que sobraria um camelo de qualquer modo. Na verdade X/2+X/3+X/9 = 34/36 = 17*X/18.

Ora se ao invés de 18 camelos tivéssemos 36 camelos (X=36) então X/2+X/3+X/9 = 34. Ou seja sobrariam 2 camelos. E o irmão mais velho receberia 18, o do meio 12 e o mais novo 4. O que fazer com os dois camelos? Ora eles não fariam parte da partilha de qualquer modo…

Já se a partilha fosse X/2, X/3 e X/6, então o matemático ficaria sem seu camelo, pois neste caso o irmão mais velho receberia 18, o do meio 12 e o mais novo 6. E 18+12+6 é 36.